Home Page (MVA) > Integrated Assessment Models (IAMs) and Resources > IAMs Thematic Guide
GENERAL DISTRIBUTION
OCDE/GD(94)75
TECHNICAL PAPERS
N° 97
THE OECD GREEN MODEL:
AN UPDATED OVERVIEW
by
Hiro Lee, Joaquim Oliveira-Martins, and Dominique van der Mensbrugghe
Produced as part of the research programme on Sustainable Development: Environment, Resource Use, Technology and Trade
ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT
Paris 1994
015327
CENTRE DE DÉVELOPPEMENT DOCUMENTS TECHNIQUES
Cette série de documents techniques a pour but de diffuser rapidement auprès des spécialistes dans les domaines concernés les résultats des travaux de recherche du Centre de Développement. Ces documents ne sont disponibles que dans leur langue originale, anglais ou français; un résumé du document est rédigé dans l'autre langue.
Tout commentaire relatif à ce document peut être adressé au Centre de Développement de l'OCDE, 94 rue Chardon Lagache, 75016 Paris, France. Un certain nombre d'exemplaires supplémentaires sont disponibles sur demande.
DEVELOPMENT CENTRE TECHNICAL PAPERS
This series of technical papers is intended to disseminate rapidly the Development Centre's research findings among specialists in the field concerned. These papers are generally available in the original English or French, with a summary in the other language.
Comments on this paper would be welcome and should be sent to the OECD Development Centre, 94 rue Chardon Lagache, 75016 Paris, France. A limited number of additional copies of this paper can be supplied on request.
TABLE OF CONTENTS
ILLUSTRATIVE POLICY SIMULATIONS
The authors gratefully acknowledge the support and advice of Peter Sturm and David Roland-Holst during the latest phase of the GREEN project. We also would like to thank Colm Foy and David Turnham for their useful and insightful remarks on the previous version of this paper. Finally, we extend our appreciation to GREEN workshop participants at MIT, Stanford University, the World Bank, the Kiel Institute, the Research Center in J<ü>lich, and the OECD.
Cet ouvrage est destiné àservir d'introduction au modèle GREEN de l'OCDE. Le modèle GREEN a été développé par le Secrétariat de l'OCDE afin de mesurer l'impact économique de différentes politiques de limitation des émissions de CO2. Cet ouvrage comporte deux parties. La première décrit la structure du modèle. La seconde présente plusieurs résultats du modèle, dont notamment la simulation de référence et des simulations alternatives de limitation des émissions de carbone. Les lecteurs intéressés par la structure détaillée du modèle ou son utilisation sont invités à se référer aux manuels préparés à l'intention des utilisateurs.
This paper presents a brief introduction to the OECD GREEN Model. The GREEN model has been developed by the OECD Secretariat in order to assess the economic impact of abating CO2 emissions using several different economic instruments. The paper is divided into two parts. The first provides a brief introduction to the structure of the GREEN model. The second describes several different simulations using the GREEN model, including what is generally referred to as the Business-as-Usual scenario and several alternative carbon-abatement scenarios. For specific details on the model and its implementation, readers are referred to the GREEN Reference Manual, and the GREEN User Manual.
This Technical Paper, prepared as part of the Development Centre's research programme on "Sustainable Development: Environment, Resource Use, Technology, and Trade", presents an overview of the current version of the OECD GREEN model, and an up-to-date report of the key simulation results of the economic costs of reducing carbon emissions.
Environmental issues have entered the mainstream international economic policy arena with increasing urgency over the last decade. The Rio "Earth Summit", held in June 1992, was an important milestone in the debate, bringing together the largest coalition of countries ever to discuss global environmental concerns. One of the more prominent topics of debate is the issue of global warming which is generated by increasing concentrations in the atmosphere of carbon dioxide, and other so-called greenhouse gases. Over the last three years, the OECD Secretariat has devoted a major effort to analysing the economic costs and consequences of limiting carbon emissions, primarily generated by the consumption of fossil fuels.
The scope of the OECD GREEN model is global, and therefore, the model results show the increasing importance of non-OECD countries in the growth rate of carbon emissions, the distributional impacts of reaching an agreement on their limitation, and several policy alternatives for mitigating the economic costs of a carbon tax on fuels. The GREEN model has a rich set of policy instruments, as well as many exogenous elements which allow the policy analyst to experiment with many different facets of the global warming issue. Some of the most important factors include population and GDP growth rates, energy efficiency improvements, and the cost and availability of alternative energy sources in the future. The GREEN model is now available to all interested users, and we hope it will provide a useful instrument in informing the policy dialogue on the global warming issue.
Jean Bonvin
President, OECD Development Centre
July 1994
The GeneRal Equilibrium ENvironmental model, hereafter referred to as GREEN, was developed by the OECD Secretariat in order to assess the economic impacts of imposing limits on carbon emissions. The model was developed in the period 1991-92 and has been used extensively for a wide variety of analyses including the impacts of emissions constraint in the OECD, global agreements, tradable permits, transfer mechanisms, and comparisons with other carbon abatement models. A description of the model, and many of the basic analyses are reported in several papers in a special issue of OECD Economic Studies (1992). Background material can be found in the Working Paper series of the OECD Economics Department, particularly Burniaux et. al. (1992). The model comparison exercise is summarized in OECD (1993).
The GREEN model has been updated over the last year, and documentation has been prepared to make the model available to outside users. There have been changes in the specification of the model, in the specification of the baseline scenario, and in the data. This paper is intended to provide a general introduction to the model specification and an update of some of the key results.
The paper is divided into two parts. The first provides a general introduction to the model specification. For a full description of the model structure and its implementation, readers are referred to Burniaux et. al. (1992), and van der Mensbrugghe (1994). The second part of the paper describes some of the key results from the basic simulations of the GREEN model, including the reference, or baseline scenario, OECD carbon emission stabilization, and a global co-operative agreement to limit carbon emissions. The simulations are intended to show some of the key mechanisms of the GREEN model, and some of the policy issues which can be addressed by the model.
*Hiro Lee, OECD Economics Department and University of California, Irvine. Joaquim Oliveira-Martins, OECD Economics Department. Dominique van der Mensbrugghe, OECD Development Centre. The views expressed in the paper are those of the authors and do not necessarily reflect the views of the OECD. Correspondence can be addressed to any of the authors at the OECD, 2 rue André-Pascal, 75775 Paris Cedex 16, France.GREEN is a recursive-dynamic global computable general equilibrium (CGE) model with a special focus on energy production and consumption. The model is calibrated on a 1985 data set, and is calibrated dynamically to produce an exogenously given path of real GDP growth and population growth. The description of the model is divided into four sections. The first section describes the different dimensions of GREEN. The second section describes the single-period (or static) specification of the model. The third section describes the dynamic features of GREEN. The final section discusses some of the features of the model's implementation.
Regions
Global economic activity is divided into twelve regions, each one modeled similarly, albeit with a different base data set and a different set of parameters. Four of the twelve regions are composed of OECD Member countries (see Table 1). They are the United States (USA), Japan (JPN), the European Community (EEC), and the rest of the OECD (OOE), which includes the EFTA countries, Canada, Australia, and New Zealand. The formerly planned economies of Europe have been divided into two regions--the former Soviet Union (FSU), and Eastern and Central European Economies (EET). The rest of the world is comprised by six regions, including three large single countries--China (CHN), India (IND), and Brazil (BRA). All other countries are aggregated into three regions. One region is comprised of the Dynamic Asian Economies (DAE). Another region includes the major energy-exporting countries (EEX). The final region contains all other countries and is designated as the rest-of-the-world (ROW). In 1985, the ROW region represented approximately 5.3 per cent of world GDP and 5.4 per cent of world CO2 emissions.
Sectors
Economic activity is initially divided into eight sectors, with seven energy backstop substitutes introduced in later years. The initial sectors include five energy-based sectors, and three other sectors (see Table 2). The energy sectors are coal, crude oil, natural gas, refined petroleum products, and electricity (which--for data reasons--also includes gas and water distribution). The remaining sectors are agriculture, energy-intensive industries, and all other goods and services.
The model incorporates energy backstop substitutes. These are sources of energy which are expected to be available in the future. There are seven backstop energies. Coal, crude oil, and natural gas, are each assumed to have two substitute fuels--one which is carbon intensive, such as tar sands, and one which is carbon-free, such as biomass. Electricity has one backstop energy substitute, which is assumed to be a carbon-free source, such as fusion, solar, wind, etc.
Time dimension
GREEN is a recursive dynamic model, i.e. each period of the model is solved as a single period model, with backward looking transition equations linking the individual periods together. The key transition equations include labour growth, capital accumulation, fossil fuel resource depletion, and energy and factor efficiency improvements. Changes in policies are assumed not to change the growth of labour and the efficiency factors, but will affect the growth and composition of the capital stock to the extent that these policies change domestic saving. The solution periods are 1985, 1990, 1995, 2000, 2005, 2010, 2030, and 2050, i.e. the step-sizes are initially five years, and beyond 2010, twenty year steps.
Factors of production
The model has three kinds of factors of production: labour, capital, and sector-specific fixed factors. Labour supply is assumed to be exogenously given in each region (in each period), perfectly mobile across sectors, and therefore, associated with a single economy-wide wage rate.
Capital is divided into vintages: old and new. Substitution possibilities are allowed to differ between old and new capital, with typically lower substitution elasticities on old capital. This type of structure of capital is often referred to as putty/semi-putty. New capital is assumed to be perfectly mobile across sectors and available at a single economy-wide rate of return. Vintage (or installed) capital is partially mobile. Sectors in decline--which are identified with a declining demand for capital--are assumed to supply old capital which is made available to all the expanding sectors. The supply of disinvested old capital is assumed to be perfectly homogeneous with new capital, and hence is available at the same price.1 The price of old capital in declining sectors is assumed to be sector-specific. In total, the number of factor prices on the capital market will equal one plus the number of sectors in decline. The supply of so-called new capital includes capital from new investments, plus capital sold by sectors in decline, plus installed capital from sectors in expansion.
Five of the eight sectors have a sector-specific factor. In agriculture it is land. In coal, crude oil, and natural gas, it is the reserves of the base product. In electricity, it is the capital installed in the electricity sector which is associated with the carbon-free production of electricity, i.e. nuclear power plants, hydro-electric dams, and geothermal sources. The fixed factors in agriculture, coal, and electricity are assumed to be available using an upward sloping supply schedule, with different supply elasticities depending on whether demand for the factor is increasing or decreasing. For example, it is assumed that it is easier to decrease the supply of land in agriculture, than to increase it. Resource depletion models have been developed for the crude oil and natural gas sector which will be further described below.
GREEN is a recursive dynamic model. As such, the solution for each period of the model can be solved independently of any future period, there is no forward looking behaviour. The periods are linked together through factor-accumulation equations which can be either exogenous, as the case for labour supply, or endogenous, as is the case for capital supply and resource depletion.
This section will describe the main elements of the static solution of the model, i.e. the specification of the model which deals with the single-period solution.
Production
There are two main characteristics of the production structure in GREEN--the putty/semi-putty specification of production, and the multi-level nesting of the inputs of the production structure.
Within each period, capital is classified as being either old (installed) or new. New capital is mainly generated by the previous period's investment. This vintage structure of capital allows for differentiating the substitution possibilities across inputs by the age of capital. Typically, the substitution elasticities are lower for old capital, than they are for new capital. The aggregate substitution possibilities will be an average of the two, weighted by the respective shares of old and new capital in total capital.
Figure 1a and 1b depict the nesting and substitution possibilities of the production function. The top level starts with a Leontief structure in non-energy intermediate inputs and a capital-labour plus energy bundle, which is designated by the variable KLEF (capital-labour-energy-fixed factor). The second level disaggregates the KLEF bundle into labour and a capital-energy-fixed factor bundle (KEF). The functional form used is known as the constant-elasticity-of-substitution function (CES), and the substitution elasticity is generally lower for production using old capital, than production using new capital. The third level of nesting splits the KEF bundle into an energy bundle and a KF (capital-fixed factor) bundle. The fourth level of nesting splits the KF bundle into capital and the fixed factor. A Leontief technology is assumed here, i.e. capital and the fixed factor are always used in constant proportions. This implies perfect complementarity between the two.
The energy bundle is divided into its various components with another multi-level nesting structure (see Figure 1b). The top level energy bundle eventually splits into demand for twelve basic fuels: coal and its two backstop substitutes; crude oil and its two backstop substitutes; natural gas and its two backstop substitutes; refined oil; and electricity and its single backstop substitute.
The first level in the energy nest is the division of energy demand into an electric component and a non-electric component. The second level divides the non-electric component into a coal component and a oil plus gas component. The third level disaggregates the oil plus gas bundle into three components: crude oil, natural gas, and refined oil. At this stage, demand for five fuel composites has been determined: coal, crude oil, natural gas, refined oil, and electricity. If the backstops are not available, the demand for these fuel composites is identically equal to the demand for the conventional fuel equivalents. With the introduction of the backstop fuels, demand for the fuel composites will be allocated across the conventional fuel and the available backstops, using a CES cost-minimisation function. Hence the coal, crude oil, and natural gas fuel composites will each be disaggregated into a conventional fuel component and two backstop demands--a carbon-based backstop fuel, and a carbon-free backstop fuel. There are no backstop substitutes for refined oil since it is a processed fuel which is derived from either crude oil or the backstops. The demand for the electric composite will be split into demand for conventional electricity and the backstop electric option.
In conclusion, starting from a given output (by vintage), the producer will minimise the cost of producing that output using the multi-tiered nested function. At the end of the nesting, the producer generates demand for the 15 commodities of GREEN--3 non-energy commodities, and 12 energy-based commodities--labour, capital, and the fixed factor. Given the assumption of constant returns to scale, the producer price is set to the unit cost of production (taking into account production taxes/subsidies) .
Consumption
Each region has one representative consumer (household), which receives all the income generated by value added, i.e. both labour and capital income (including income generated by the sector specific fixed factors). The GREEN model uses a static version of the extended linear expenditure system (ELES) to determine the optimal allocation of the consumer's disposable income for consumer goods and household saving.2 The definition of consumer goods differs from the definition of production goods. There are four consumer goods. They are Food and Beverages, Fuels and Power, Transport and Communication, Other Goods and Services. The four consumer goods are transformed from producer goods using a type of make matrix, or a consumer-production technology (see Figure 2). Each of the four consumer goods is made up of a non-energy bundle and an energy bundle using a fixed coefficients (or Leontief) technology. The energy bundle is dis-aggregated into the various base fuel demands using the same type of nesting as in production, albeit with potentially different substitution elasticities and share parameters.
Other Final Demand Activities
There are three final demand activities other than households: government expenditure on goods and services, labour, and capital; investment final demand; and change in stock levels (which is assumed to be at a zero activity level after the base year).
Government revenues are generated by indirect taxes, direct taxes on households, and fuel taxes. Real government expenditures are assumed to grow at the same rate as GDP. The government allocates its expenditures using a three-factor CES production technology -- aggregate goods and services, labour, and capital. Goods and services are further dis-aggregated using a fixed coefficient technology for non-energy goods and an energy bundle. The energy bundle is dis-aggregated using the same nesting as in production (see Figure 1 b). (The government's production function is also split into old and new capital, but for many regions there is no estimate on capital use in the government sector, hence this has little effect. Further, the substitution parameters used in the reference version of the model are equal across vintages.)
Investment final demand also uses a fixed coefficients expenditure function in non-energy goods and an energy bundle. The energy bundle is dis-aggregated using the same nesting as all the other agents in the economy. Government and investment closure will be discussed below.
Trade
Trade is modeled using the so-called Armington assumption. Each commodity is assumed to be differentiated by region of origin. In GREEN, this implies a two-level nest (see Figure 3). At the top, each agent in the economy generates an aggregate demand for a good. At the next level, agents split the demand for the aggregate good into a domestic component and an aggregate import component. In GREEN, the CES expenditure function is used as the Armington aggregation function. At the next level, the aggregate import demand is distributed across the regions of the model. As an example, assume consumers generate a demand for automobiles (in aggregate) using the ELES function. At a second stage, consumers will split this aggregate demand into demand for domestic cars and aggregate import cars, using a CES function which represents their preferences. Finally, at the last stage, consumers will divide aggregate import demand for cars across the countries of origin of the cars -- Japan, Germany, Italy, etc. -- again based on a CES function which represents their preferences.3
The Armington assumption reflects two observations concerning the modeling of trade. First, two-way trade is observed in virtually all statistical trade data, which to a large extent reflects the problem of aggregating data. Next, without a sector-specific factor of production, homogeneity of products would lead to complete specialization which is rarely observed at the level of aggregation of a model such as GREEN. Note that the Armington assumption implies that there is no unique world price for a commodity. Each region's vector of world prices will differ depending on the allocation of its import demand across the other regions.
The Armington assumption is not used for all commodities. Because of its significant homogeneity, the existence of a reference world price, and relatively low transportation costs, crude oil is not differentiated by region of origin. Hence, no trade matrix exists for crude oil, and a region's net trade position is simply the difference between its supply and demand. If supply is greater than demand, the region is a net exporter, otherwise, it is a net importer. The significant transportation costs of natural gas and coal means that these commodities are assumed to be Armington goods, with the transportation costs proxied by the imperfect substitutability of the goods.
The backstop fuels are also not Armington goods, in fact, they are assumed not to be traded at all. The backstop fuels are assumed to be available in unlimited quantities in all regions, at a given fixed price which is the same in all regions.4 As a consequence of this assumption, there is no incentive to trade in these fuels.
Export demand in any given region is simply determined by the sum of import demand from all the other regions of the model 5 Export supply is identically set equal to export demand. There is no assumption about strategic behaviour on the part of exporters.6
Closure
There are three closure rules in GREEN -- the net government balance, investment-savings, and the trade balance. The net government balance position is under user control, but in the reference version of the model, it is assumed that the net position of the government is fixed (in real terms) at its base year level. This implies that the household tax schedule shifts in or out in order to achieve the exogenously given government budget position.
There is no investment schedule in GREEN. Domestic investment is identically equal to the sum of domestic saving resources, i.e. household saving, government saving, and net foreign saving. When government saving as well as foreign saving are exogenous, changes in investment are mostly determined by changes in the level of household saving.
The final closure rule concerns the trade balance. The trade balance is assumed to be fixed in each period for each region (in real terms).7 This closure rule implies that the real exchange rate is the equilibrating mechanism for maintaining the trade balance. For example, if a region liberalises its trade regime (by lowering its tariffs), it will be forced to lower its real exchange rate in order to be able to export more and maintain a constant trade balance.
GREEN is a Walrasian model, so the vector of prices is only solved for in relative terms. One price needs to be chosen as the numéraire. The OECD GDP price deflator has been chosen as the numéraire because of the relative ease in interpreting the results with respect to this price index.
Emissions and carbon taxes
GREEN computes carbon emissions which are generated by the consumption of carbon-based fuels -- coal, crude oil, natural gas, refined oil, and the carbon-based backstops. The consumption of electricity and the electric backstop do not generate CO2 emissions directly.8 Consumption of the carbon-based fuels is aggregated over all sources of demand, both intermediate and final, and converted into emissions.9 Due to calibration rules, all volumes are expressed in millions of 1985 dollars, and not in physical quantities, such as exajoules, or tonnes. In order to calculate carbon emissions, volumes are converted from millions of 1985 dollars to exajoules using conversion factors which are calculated from the base-year data. The exajoule consumption is then converted into emissions, using constant fuel-specific emission factors (which are expressed in terms of millions of tons of carbon per exajoule of consumption). The emission factors are highest for coal, followed by oil, and then natural gas.10.
In the business-as-usual scenario, there is no policy initiative to reduce carbon emissions, and the model simply adds up the emissions in an accounting identity. In policy simulations, carbon and/or energy taxes are introduced in order to limit the quantity of emissions. The equilibrium taxes are the shadow price of the carbon emission constraint. The model allows for a wide variety of definitions of the constraints, and therefore, the taxes. The emission constraints can be specified over individual regions (generating region-specific taxes), or over an aggregation of regions (generating a single tax over the defined aggregation). The emission constraints can be specified with respect to the emissions of any past period. The user can specify transfer (or recycling) schemes in order to modify the distribution of the costs. Finally, the model allows for tradable permits, where each region is allocated an initial quota of emission rights which can be traded. The distribution of losses will clearly depend on the initial allocation rights.
Capital
The vintage structure of capital has already been mentioned above. At the beginning of each new period, capital is divided into two categories, old and new. Old capital is all of the previous period's installed capital, depreciated at a constant given rate of depreciation. There are two features of old capital. First, it is less substitutable with the other factors of production and energy, than new capital.11 Second, it is partially immobile reflecting the potentially significant costs of moving installed capital from one sector to another. New capital is generated by the previous period's investment. It is assumed that new capital is perfectly mobile and will be allocated across sectors in order to equalise its rate of return across sectors. If a sector is in decline, or in other words, if a sector has too much installed capital to produce the output which is demanded, it will sell some of its installed capital to expanding sectors. Because of the costs of moving capital across sectors, the supply of dis-invested capital only responds partially to differentials in the relative rates of return of the sector-specific rental rate on old capital, and the economy-wide new capital rental rate. It is assumed that disinvested capital is homogenous with new capital, i.e. it is added to the stock of new capital, and hence has the same rate of return as new capital.
Depletion
The GREEN model incorporates resource depletion modules for crude oil and natural gas.12 For each of the two fuels, the model keeps track of two reserves: proven and yet-to-find potential reserves. Production from proven reserves is assumed to be a fixed share of proven reserves, which is invariant over time. Yet-to-find reserves are fixed in the base period, and each year a proportion of yet-to-find reserves is converted into proven reserves. The dynamics between the two reserves generate a production profile which initially is independent of prices. If prices do not change, or producers are insensitive to changes in prices, the production path of both fuels is fully deterministic and can be traced out in the base year. Depending on the extraction rate (from proven reserves), and the conversion rate (from unproven to proven) reserves, regions can either be faced with monotonically downward production profiles, or skewed-bell shape profiles (see figure 4a and figure 4b). In the latter case, unproven reserves are being converted into proven reserves at a rate which is greater than production. At some time in the future, however, unproven reserves decline to the point where all regions will be on the downward slope of production .
GREEN relaxes these assumptions in two ways. The conversion rate is price sensitive. The intuition is that if prices rise (fall), this induces producers to increase (decrease) the rate of conversion (or the rate of discovery). The parameters defining the rate of discovery function are calibrated to match production scenarios from energy experts. GREEN also allows producers to make their supply decisions based on the level of the world oil price, in other words, producers are allowed to produce below their production profiles, if the price incentives are lacking.13 In no case is a region able to produce beyond the potential production profile.
Technology changes
GREEN has three sources of technology changes: labour, capital, and energy. Changes in labour efficiency are assumed to be exogenous, and they are specified by the user.14 Changes in energy efficiency are also exogenous, and obviously represent a key component in determining the level of energy use and emissions. This parameter, sometimes referred to as the Autonomous Energy Efficiency Improvement (AEEI) parameter, is implemented as specific to the region, the sector, the capital vintage, and time. For tractability (and comparison with other models), a uniform value of 1 per cent has been chosen for the reference simulation.15
The capital efficiency parameter is calibrated in the business-as-usual simulation in order to insure that the model generates balanced growth, i.e. the capital-labour ratio (in efficiency terms) remains constant.16 Another way of looking at this dynamic calibration procedure is to think in terms of targets and instruments. The target is a specified growth rate of real GDP. This factor has been chosen as the instrument to achieve the exogenously specified growth rate. In all policy simulations, the capital efficiency parameter is exogenous.
The GREEN model is calibrated to a 1985 data set. The necessary data to put together a model like GREEN include input/output tables, national income and product accounts, detailed energy statistics, and tables of world trade flows. The key parameters of the model essentially substitution, supply, and income elasticities were derived from an exhaustive literature search, and are described fully in Burniaux et. al. (1992). All other parameters - mainly shift and share parameters are calibrated in the base year using the key parameters and the base data.
The GREEN model is coded in a procedural language, C, rather than an equation-solver package.17 Thus, the model implementation requires not only the specification of the model, but the specification of the solution algorithm as well. Gauss-Seidel was chosen because it is relatively simple to implement, and compact. Two issues arise in Gauss-Seidel: the ordering of the equations, and the determination of equilibrium prices. The ordering of the equations is determined to a large extent by the recursive nature of the model (see the GREEN Reference Manual). Changes in the ordering can have serious consequences on the convergence properties of the solution algorithm.
Gauss-Seidel requires that all endogenous variables, appear at least once on the left-hand side of an equation. Since factor prices (and potentially other equilibrium prices, such as the price of oil), are determined by equilibrium conditions, they do not naturally appear on the left-hand side of an equation. Equilibrium conditions are therefore transformed into excess-demand equations, and equilibrium prices are updated in each iteration depending on the direction and extent of the excess demand. For example, the wage equation is:
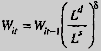
where W is the wage rate, it is the iteration counter, Ld is labour demand, Ls is labour supply, and delta is referred to as the damping factor. Clearly, in equilibrium, this equation is equivalent to the following:
Ls = Ld
If in an intermediate iteration, labour demand exceeds labour supply, the tatonnement equation will raise the wage rate, which, all else being equal, would lead to a reduction in labour demand, i.e. a reduction in the excess demand. It turns out that the key variable in the tatonnement equation is the damping factor. A factor which is too high can lead the algorithm to explode. A factor which is too low can lead to very long convergence cycles. Since there are numerous equilibrium equations in the model, all interfering with one another, choosing the best set of damping factors is more art than science.
Solution in a single period requires the solution of between 25,000-35,000 non-linear equations (depending on the user-specified options). On a 80486-equipped PC, it takes anywhere from 30-60 minutes to solve the full model (7 periods). On an HP work station, it takes from 6-10 minutes. Since the model is written in C, it is highly portable.
Illustrative Policy Simulations
This part of the paper will present the results of a few illustrative simulations using the GREEN model. The first section describes the reference scenario, also known as the baseline scenario. Several key results will be highlighted, particularly energy consumption and the pattern of carbon emissions. Variants on the baseline scenario will be presented, to show the sensitivity of the model to several key assumptions. The second section will present some scenarios of carbon emissions stabilisation which is limited to the OECD regions. One of the aims of this section is to highlight the increasing importance of CO2 emissions generated outside the OECD region, and the efficiency improvements from enacting a co-ordinated policy of abatement, over a go-it-alone approach. The third section will describe some simulations with world-wide co-operation. This section will highlight some of the issues of equity, as well as efficiency.
As a first step in analysing the impacts of CO2 abatement policies, it is necessary to develop a reasonable reference, or baseline, scenario. 18 Changes in abatement policies are then compared to the reference scenario. Many exogenous elements are part of the reference scenario and these have been somewhat modified from previous analyses using the GREEN model, particularly with respect to the results presented in OECD (1992). The modification with the most importance, is the phasing out of fossil fuel subsidies in all countries by the year 2010. Another important difference in the baseline scenario is the change in the GDP growth rate assumptions for China and the former Soviet Union in order to take into account recent trends. The final significant modification is the reduction of the substitution elasticity and the penetration share for the electric backstop option. The following list indicates the main exogenous elements for the baseline scenario described below.
- A consensus growth path for GDP and labour (population) is garnered from other models (for comparison purposes) and/or projections from international institutions, such as the UN or the World Bank. Table 3 and Table 4 provide the projections for labour and GDP for the current baseline scenario. World population growth slows from the current 1.6-1.8 per cent growth per annum (p.a.) to 0.7 per cent. The growth rates are highly differentiated by region. For example, the OECD population growth rate is projected to be negative between 2030 and 2050, while it will be around 0.7 per cent for the non-OECD area. In absolute numbers, world population will grow from 5.26 billion persons in 1990 to almost 10 billion by the year 2050. Growth in world GDP is projected to slow down, from roughly 3.0 per cent currently, to around 2.2 per cent between the period 2030 and 2050. The GDP growth rates are also differentiated by region. Overall, this implies that GDP in the year 2050 will be about 5 times its level in the base year, 1985. Per capita GDP will increase from around $2,500 to $6,300 (in 1985 US dollars), a 2.5 times increase over the 65 years. Labour efficiency (as stated above) is assumed to be exogenous, and capital efficiency is calibrated in order to achieve the targeted real GDP growth rate.
- Energy efficiency is assumed to increase by 1 per cent per annum, by all consumers of energy, except in the production of fossil fuels and refined oil.
- Existing energy distortions play a major role in determining the level and pattern of energy consumption. The energy distortions have been determined by comparing world prices with domestic prices (using the available nominal exchange rates). Table 5 presents the level of distortions assumed in the base year data. Many OECD regions tend to tax fossil fuels, domestic prices are higher than world prices. Several significant non-OECD regions have large implied subsidies on fossil fuels. Coal consumption is heavily subsidised in China, the former Soviet Union and Central and Eastern Europe, and India. The former Soviet Union has particularly high subsidies in crude oil and natural gas. Due to the currently observed changes in many regions and the problems of sustaining such large distortions over time, it is assumed, in the baseline scenario, that subsidies on crude oil are phased out by the year 2000, and the subsidies on coal and natural gas are phased out by the year 2010. Fossil fuel taxes are not modified.
- Table 6 presents the backstop assumptions for the baseline scenario. All backstops are assumed to become available in unlimited quantities in the year 2010. The price of the carbon-based backstop corresponds to an equivalent of $50 per barrel of crude oil. The price of the carbon-free backstop is twice as much. The electric backstop is priced at the equivalent of 7 1/2 cents per Kwh. The market share of the backstops will also depend on their degree of substitutability with the conventional fuels, and the penetration shares. Both of these parameters are specified by the user.
- Foreign savings are assumed to be held fixed at their base-year level (in real terms). The real exchange rate is the equilibrating mechanism in this case. Government savings are also fixed at their base-year level, with the household direct tax schedule the equilibrating mechanism for this closure rule.
- The world price of oil is determined endogenously. All regions are assumed to be on the potential production profile except the energy exporting region (EEX), which is assumed to have a price sensitive supply curve until it hits its production capacity limit.
Baseline Scenario with Distortion removal
Given this scenario, the model generates the levels and patterns of energy consumption as depicted in Table 7. Energy consumption is projected to increase by a factor of 3.2 between 1985 and 2050, which implies an annual increase of 1.8 per cent per annum. Energy consumption is almost evenly divided between the OECD and non-OECD regions in the base year, which reflects significant energy efficiency gains in the OECD countries. By the year 2050, the non-OECD regions consume over 60 per cent of global energy. In 1985, crude oil accounts for almost 40 per cent of total primary energy consumption, followed by coal, with a 33 per cent share, and natural gas with almost a 23 per cent share. Carbon-free sources of energy account for less than 5 per cent of the total. These shares change considerably by the year 2050. Coal consumption dominates total energy use with a 42 per cent share. Coal is relatively abundant, particularly in some of the large regions, keeping its price relatively low. The crude oil share drops from 40 per cent to 28 per cent, and natural gas drops from 23 per cent to 15 per cent. The carbon-based backstop garners a 10 per cent share of total energy use in the year 2050. Mainly, it is used as a substitute for crude oil, whose price increases by more than 100 per cent (as compared to the average OECD GDP price deflator), between 1990 and 2050. The electric backstop option only penetrates the Japanese market, due to the already high cost of producing conventional electricity in Japan.
The pattern of carbon emissions, will evolve in the same direction, albeit, weighted by the relative carbon intensity of the respective fuels. In the base year, coal consumption accounted for 42 per cent of total carbon emissions, crude oil 42 per cent as well, and natural gas 16 per cent (see Table 8). The non-OECD regions accounted for a slightly greater share of emissions than energy consumption, 51.2 per cent, instead of 49.7 per cent, reflecting the higher use of coal. The largest emitters in the base year are USA (24 per cent), FSU (18 per cent), EEC (14.4 per cent), and China (9.5 per cent). The shares reflect both the size of these economies, and the patterns of energy consumption. The growth rate in total emissions follows the same trend as the growth in total energy. However, because of the higher concentration of coal consumption in the non-OECD countries, they are responsible for almost two-thirds of total carbon emissions by the year 2050.
Baseline with No-distortion removal
Results in this section briefly indicate the impact of distortions on overall energy use and the patterns of energy consumption and emissions. The only difference between the no phase-out baseline scenario in this section, and the previous baseline scenario is that the energy subsidies observed in the base year are maintained throughout the entire period, i.e. there is no phasing out of the energy subsidies by the year 2010.
The results on the energy and emissions patterns are presented in Table 9. (There being no difference in the base year, only the patterns for the year 2050 are presented.) Energy consumption in the year 2050 is 34 per cent greater when the energy subsidies are maintained at their existing base levels, than in the baseline scenario where they are phased out. Similarly, under the no phase-out scenario, carbon emissions are 41 per cent higher. This is in large part due to the higher concentration of coal consumption in those countries with significant subsidies. Under the initial baseline scenario, coal consumption represents a 42 per cent share of total energy consumption in the year 2050. Under the no phase-out scenario, the share of coal in total energy consumption increases to 66 percent. Some of the regional differences are striking as well. The non-OECD share of emissions increases from 66 per cent to 75 per cent, with China's share in particular increasing from 18 per cent to 30 per cent. These results emphasize the need for energy price reform, not only from a fiscal and efficiency point of view, but also because of the potential significant harm to the global environment.
Changes in energy efficiency
This section describes the sensitivity of the baseline results with respect to the AEEI parameter. Results from using two different values for the AEEI are reported. The AEEI was first doubled, i.e. a two-fold increase in the growth of energy efficiency, and then reduced by 50 per cent.
An AEEI of 2 per cent leads to a significant reduction in energy use and emissions. However, because of the general equilibrium nature of the model, the reductions are to some extent dampened by two effects. The first is an income effect deriving from the fact that increasing efficiency increases income, all else being equal. The second is a substitution effect. Since demand for energy is tempered, its price will be lower, all else being equal, hence, there will be a movement down the demand curve. An AEEI of 0.5 per cent has the opposite effect, it will tend to increase energy demand compared to an AEEI of 1 per cent.
Figure 5 depicts the differences in carbon emissions between the three values of the AEEI. Clearly, in no case would even the higher value of 2 per cent project a stabilisation in emissions close to the Toronto-type target. With an AEEI of 2 per cent, global energy demand is only 621 exajoules in 2050, a reduction of 29 per cent from the baseline scenario, and global emissions are down 26 per cent, to 12,667 millions of metric tons (Mmt). With the more pessimistic value of 0.5 per cent, energy demand increases by 12 per cent, to 984 exajoules, and global carbon emissions increase by 15 per cent to 19,628 Mmt. It is difficult to conceive of a significant breakthrough in the fossil fuel technology which would reduce carbon emissions to the levels suggested by a Toronto-type target.
Stabilisation of Emissions in the OECD
This section describes some of the key results from imposing stabilisation of emissions in the four OECD regions of the GREEN model. The first part imposes a region-specific constraint in each of the four regions, and hence region-specific carbon taxes. Next an OECD-wide stabilisation constraint is imposed, and therefore, an OECD-wide tax. The difference in the two results indicates the efficiency gains from a multi-lateral agreement. Table 10 presents the patterns of emissions in the OECD regions for both simulations. In both cases the overall level of emissions is identical, but the regional distribution of emissions and costs will change.
Region-specific taxes
In the first simulation, each OECD region imposes a stabilisation target, starting in 1995, at the 1990 level of emissions. This target is held constant through 2050. This results in a reduction of 52 per cent in OECD emissions in the year 2050 as compared to the baseline level of emissions, but overall, emissions drop by only 18 per cent in 2050 compared to the baseline. It has relatively little impact on emissions in the non-OECD regions. These regions are able to switch to less polluting sources of energy, such as crude oil, as its relative price drops.
The carbon taxes represent the shadow price of the carbon constraint in each region. The level of the carbon tax will be influenced by each region's mix of fuels, the carbon intensity of the fuel mix, the level of the target, and the inter-fuel substitution possibilities. Table 11 gives the level of the carbon taxes (in 1985 US dollars per ton of carbon emitted, and deflated by the regional GDP deflator, also depicted in Figure 6). For three of the four regions, the carbon tax varies in a relatively narrow band which starts at $30-50 and rises to $120-160 towards 2050. The costs in Japan are distinctly higher, starting out at $145, rising to $339 in 2005, dropping precipitously in 2010, and rising again to $305 by the year 2050. The drop in the year 2010 arises from the introduction of the electric carbon-free backstop which allows Japan to shift to a carbon-free source of energy. The backstops effectively put a break on changes in energy prices since they are available in unlimited quantities at a fixed price. Therefore, as the target becomes more binding, most of the adjustment must occur in the level of the taxes, rather than in the price of the fuels.
The repercussions in terms of real income are presented in Table 12.19 The major sources of change derive from the familiar distortionary triangles associated with imposing taxes, and changes in the terms of trade. The changes in real income in the initial periods are relatively modest for all regions except for Japan where the large size of the tax takes an early bite. The United States even has a slight gain in 1995 as the costs of the tax are outweighed by the positive gains in the terms of trade as the world price of oil is deflated by the drop in oil demand. In the year 2050, the losses, compared to the baseline scenario range from 1.1 per cent in the Other OECD region to 3.1 per cent in Japan. Japan has to bear the largest cutback in emissions, 66 per cent. While the other regions are not participants in the stabilisation scheme, they will be affected as well, mainly through the impact of changes in world energy prices. This tends to have negative impacts on oil exporters, particularly the EEX region, but will prove beneficial for energy importers.
OECD-wide taxes
An alternative to the previous simulation, is a multi- lateral agreement to stabilise OECD-wide emissions at their 1990 levels. This implies a single OECD-wide constraint and a uniform energy tax. This obviously generates the same level of emissions, but the pattern of emissions is allowed to differ. Not surprisingly, the main beneficiary is Japan which increases its level of emissions from 333 Mmt in the previous simulation, to 497 Mmt in the current one in the year 2050. Most of the transfer occurs between the United States and Japan, with little overall impact in the other two regions. The same is true in terms of the carbon tax and the changes in real income. The uniform tax in the EEC and in the OEE region is relatively similar to the region-specific tax, and therefore there is little impact in these two regions. The impact in the United States is slightly larger, and Japan sees a reduction in its real income loss from -3.1 per cent to -2.4 per cent. There is only a slight improvement in the overall OECD loss.20
While the two simulations distinguish the benefits to be delivered from multilateral agreements, they also clearly indicate that the OECD acting in concert will not be sufficient to deliver sizable reductions in global emissions. A more broad-based accord will be necessary.
This section will briefly report the results of a more broadly-based agreement to control carbon emissions. The so-called Toronto-type accord differentiates between the Annex 1 countries - the OECD plus the former Soviet Union and Eastern Europe - and the rest of the world. Under this agreement, the Annex 1 regions reduce their emissions to 80 per cent of their 1990 levels by the year 2010. The other countries are limited to 150 per cent of their 1990 level of emissions, in other words, they are allowed to expand from their current levels, but may have to cut back from their baseline levels. The first simulation describes an agreement with region-specific constraints, and no trade in emission rights. The second simulation imposes the same overall level of emissions, but allocates emission quotas based on the 80-150 scheme discussed above.
Global Accord
This section will describe the results from a global agreement to reduce carbon emissions. The Annex 1 countries commit to reducing their emissions to 80 per cent of their 1990 levels by the year 2010, while the other countries commit themselves to limiting their carbon emissions to 150 per cent of their 1990 levels by the year 2010 and beyond. This scheme of constraints leads to stabilisation of global emissions at the 1990 level, i.e. around 5,900 Mmt. Table 13 presents the results in terms of the impacts on real income. The carbon tax in the OECD regions is very high due to the significant reductions to be attained; the tax ranges from $160-280 in the four OECD regions between 2010 and 2050, with the highest tax level in Japan in 2030 and 2050. The tax rates in the non-OECD regions is relatively lower in 2010 since the constraint is not very binding, except in Brazil and the DAEs. However, by 2050, the imposed constraint becomes very stringent, and all regions have taxes of between $150 and $300, except the former Soviet Union which has a comparatively low tax of $100.
The losses in real income, overall, reach a level of 3.2 per cent in 2050, with a significantly higher loss in the non-OECD regions, -4.0 per cent, than in the OECD, -2.4 per cent. In the earlier periods, many of the non-OECD countries benefit more from the reduction in world energy prices, than they suffer from the imposition of the tax. The region with the largest loss is the energy exporting region, EEX, which could see an annual reduction in its real income of close to 10 per cent, though this is reduced to 4 per cent by the year 2050 because of a significant recovery in the price of crude oil.
Tradable permits
This simulation is similar to the previous with several differences. First, between 1995 and 2005 for the Annex 1 countries, we assume a single Annex 1-wide target and tax. In 2010 and beyond, we also assume a single world target, the same as that achieved in the previous simulation, and emission quotas are allocated to the regions of the model similar to the allocation of emission targets in the previous simulation. Annex 1 countries are given quotas which represent 80 per cent of their 1990 level of emissions, and the other countries are allocated quotas of 150 per cent of their 1990 level of emissions. Countries trade emission rights so as to equalise the marginal cost of abatement across regions. Table 14 presents the quota allocation scheme and its implications, while Table 13 contains the aggregate real income results.
The scheme - because of the efficiency generated by a uniform carbon price results in gains in global real income, compared to the previous simulation with region- specific taxes. Total losses in 2010 are only -0.7 per cent, as compared with -2.0 per cent in the previous simulation. Similar gains are made in 2030, and smaller gains in 2050. In 2050, both the OECD and non-OECD are relatively better off (in fact all regions are better off except Brazil and the DAEs). The largest gainer, compared to the previous simulation, is the EEX region, where losses are approximately cut in half.
Table 14 provides the level and values of trade in emissions. In general, the OECD regions are net buyers of emission rights, though in the later years Brazil, the DAEs, and the energy exporters buy significant emission rights. The value of trade (in 1985 dollars) starts at $47 billion in 2010, and increases to $96 billion in 2050. Despite a relatively low quota, both the former Soviet Union, and Eastern Europe are net sellers of emission rights. While it is obvious that a global agreement will lead to a more efficient outcome at the aggregate level, the initial allocation of permits clearly plays a role in determining the distribution of losses and gains across the various regions of the model.
The main purpose of the paper is to provide an updated overview of the GREEN model. Both the model structure and several illustrative policy simulations are described in order to show some of the important mechanisms of GREEN, as well as to provide a synthesis of the results of the current version of the model.
Several important elements should be retained from this presentation.
- The GREEN model is evolving over time. The structure of the model, its underlying database, and the assumptions about future trends and policies are all being constantly updated as we achieve a better understanding of the limitations of the model and the necessity of integrating the changing trends of the global economy.
- The AEEI and the assumptions on future energy price distortions play a significant role in determining the level of future emissions. While not presented, the future path of emissions is also significantly influenced by the assumptions on population and GDP growth.
- Stabilisation in the OECD countries only has a small impact on the future level of emissions in terms of the proposed Toronto-type target. If the world community has a strong commitment to reducing emissions, it will require an agreement between both the OECD countries and the non- OECD countries.
- The structure of an agreement can have a serious impact on the overall efficiency (real income gains/losses) which will be generated by abatement policies. A multilateral agreement, with a common target, and a common tax leads to an improved outcome.
- The structure of an agreement will also determine the distribution of the costs across regions. A critical element is the design of a quota allocation mechanism. Other mechanisms exist which could have the same impact, such as financial transfers. These have been explored in other studies.21
There are many other elements of the GREEN model which have not been discussed in this paper, and readers are referred to the studies listed in the bibliography. There are also many elements which are not part of GREEN, but are important parts of the greenhouse warming issue. Some of the most important include other greenhouse gases, such as SOx, NOx, and methane, the economic valuation of the benefits of abatement, and not simply the costs, and a better understanding of the backstop technologies, both from the demand and the supply side. Analysis of some of these issues is being undertaken in the OECD Secretariat as well in research institutions around the world. Given the current significant uncertainty on the physics of greenhouse warming, this issue is unlikely to disappear anytime in the near and medium term future.
AEEI
Autonomous energy efficiency improvement. The AEEI measures the change in energy efficiency, independently of other factors such as changes in relative energy prices.
Annex 1
Group of countries which includes OECD Member countries, the countries of Eastern and Central Europe, and the countries of the former Soviet Union.
AGE/CGE
Applied (or Computable) general equilibrium model.
Armington Assumption
The Armington assumption of international trade specifies that imports of similar goods coming from different countries are treated as imperfect substitutes. For example, consumers will demand energy from both domestic and imported sources which reflect differences in quality, transportation costs, and other elements which differentiate imported goods from domestic goods.
Backstop
Alternative sources of energy which are assumed to become commercially available at some future date. Examples of potential backstops include solar, bio-mass, and fusion energy.
CES
Constant elasticity of substitution function.
Closure Rule
By construction computable general equilibrium models account for all flows in an economy. The closure rules determine which macroeconomic variables are exogenous. For example, the GREEN external closure rule fixes the trade balance in real terms, and the internal closure rule fixes the government surplus/deficit in real terms.
EEC
European Economic Community.
EFTA
European Free Trade Association.
ELES
Extended linear expenditure system.
EMF-12
Stanford University-based Energy Modeling Forum, exercise No. 12.
Exajoule
One exajoule is equivalent to 1018 joules.
FCCC
Framework Convention on Climate Change. Convention debated and signed at the Rio Earth Summit, June 1992. Ratified by Annex 1 countries in March, 1994.
Gauss-Seidel
Numerical technique for finding the solution of a system of equations.
Joule
Unit of energy. In the GREEN model, each unit of fuel has a specific energy content, but all are specified in terms of joules (or more precisely exajoules). For example, one barrel of oil contains 5.736 109 joules (i.e. approximately 5.7 billion joules.)
Leontief
A Leontief structure (or Leontief production function) specifies that all inputs are used in fixed proportions (to output for example).
Mill
The equivalent to one-thousandth (0.001) of a US dollar. It is often used in specifying energy prices in terms of kilo-watt hours (Kwh). Hence 75 mills per Kwh is the equivalent of 71/2 cents per Kwh.
Mmt.
Abbreviation for millions of metric tons.
Nesting
Functional specification that assumes separability between bundles of goods, making it possible to separate optimising decisions of agents into several stages.
OECD
Organisation for Economic Co-operation and Development.
Tatonnement
A procedure used for updating prices based on excess demand conditions. If demand exceeds supply in a given market, the price in that market is increased, and the price is lowered if demand is less than supply.
Terajoule
One terajoule is equivalent to 1012 joules.
Toronto-type Agreement
Global agreement to achieve stabilisation of world carbon emissions in the future, which imposes a greater burden on the OECD countries than on the developing countries.
Tradable permits
Rights to emit a certain quantity of carbon which are tradable across countries.
BURNIAUX, J.- M., J.P. MARTIN, G. NICOLETTI, and J. OLIVEIRA-MARTINS (1992), 'GREEN -- A multi-sector, multi- region dynamic general equilibrium model for quantifying the costs of curbing CO2 emissions: a technical manual", OECD Economics Department Working Papers, No. 116, May, Paris.
BURNIAUX, J.- M., J.P. MARTIN, J. OLIVEIRA-MARTINS, and D. VAN DER MENSBRUGGHE (1994), "Carbon Abatement, Transfers and Energy Efficiency: Evidence from GREEN", in I. Goldin and L. A. Winters, editors, Sustainable Economic Development: Domestic and international Policy, Cambridge University Press, Cambridge, UK, forthcoming.
OECD (1992), OECD Economic Studies, "Special Issue: The Economic Costs of Reducing CO2 Emissions", No. 19, Winter 1992, Paris.
OECD (1993), "The Costs of Cutting Carbon Emissions: Results from Global Models", OECD Documents, Paris.
VAN DER MENSBRUGGHE, D. (1994), "GREEN: The Reference Manual", OECD Economics Department Working Papers, No. 143, Paris.
OECD (1994), "GREEN: The User Manual", mimeo, Development Centre, OECD, Paris.
Footnotes1 Installed capital in expanding sectors is also assumed to be available at the same price as new capital. This simplifying assumption enables to reduce the number of factor prices which need to be simultaneously determined in each period.
2 The ELES is similar to the more familiar LES, or Stone-Geary demand system. The main difference is the extension of the LES to a dynamic setting. The version of the ELES used in GREEN assumes myopic behaviour, so saving enters the utility function, but its determination is based only on contemporary prices (where the price of saving is assumed to be the consumer price index).
3 Unlike many CGE models, the Armington assumption holds at the level of individual agents, and not at the aggregate level. This allows substitution and import penetration shares to differ across the various agents of the economy. The drawback is that it considerably increases the quantity of information needed to calibrate the benchmark data and the number of equations in the model. For example, in a simpler CGE model, the input/output matrix requires only one set of demand equations. In GREEN, three sets are required because not only is the Armington demand calculated, but for each cell of the input/output matrix, the domestic and import content is also calculated.
4 The backstops are assumed to be available in unlimited quantities because they are either renewable fuels, such as solar, or because the resource base is so great that there is no risk of significant resource depletion within the time framework of the GREEN model. A similar assumption is made for coal reserves.
5 Because import demand of other countries is determined using the Armington assumption, exporting countries are faced with downward-sloping demand functions for their exports.
6 Some CGE models allow for the producer to differentiate between selling on the domestic market and on the world market using a so-called constant-elasticity-of-transformation function (CET).
7 The trade balance is modifiable by the user in each period. The only restriction is that the sum across all the regions of GREEN must be equal to zero. In the reference simulation, it is assumed that the trade balance is fixed at its base year level (in real terms).
8 We will use the terms carbon and CO2 emission interchangeably. However, the model only computes carbon emissions, and carbon taxes are calculated as dollars per tonne of carbon, not dollars per tonne of CO2.
9The model adjusts the emissions of the consumption of crude oil and refined oil in order to take into account the transformation process. In fact, there is almost no consumption of crude oil outside the refining sector, and hence most of the emissions generated by oil are found in refined oil consumption, and not crude oil.
10 It is assumed that the carbon-based backstop is the dirtiest (most carbon-intensive) fuel of all.
11 Because of the changing composition of old capital over time, the production share parameters are re-calibrated at the beginning of each period to reflect the evolution. The share parameters are recalibrated such that the entire stock of old capital (at the beginning of the period) can re-produce the previous period's aggregate output (using the substitution elasticities of the old capital).
12 Due to the significant stocks of coal reserves, there is no likelihood that their scarcity will become binding within the time framework of GREEN. The supply of coal reserves is price sensitive, however, with some rigidity on the upward side.
13In the implementation of GREEN, only one region has price-sensitive supply decisions, and this is the energy exporting region, EEX. All regions have price-sensitive conversion rates, but apart from this factor, all regions other than EEX are assumed to be on their production profile. An optional feature of GREEN is to specify an exogenous path for the world price of oil. In this case, the energy exporters are assumed to be a residual supplier, and there is no constraint on their productions nor is their production price-sensitive. The behaviour of the other regions remains the same.
14 Generally, due to considerations of comparison with other models, these estimates have been generated in order to be consistent with projections of world GDP.
15The only exceptions occur in the production of fossil fuels (coal, crude oil, and natural gas), and refined oil, where it is assumed to be zero.
16 Note, that the parameter is applied to the capital-fixed factor bundle, i.e. the efficiency is uniform for both factors of production. Due to this fact, there is assumed to be no efficiency growth in the fossil fuel sectors, otherwise, it would eventually be possible to produce more fuel than is available (in reserves) .
17 In part, this choice was determined by the initial availability of a model shell, and the significant size of the model.
18 The terms "reference" and "baseline" will be used interchangeably. The term "business-as-usual" is reserved for the scenario where there are no changes in energy price policies, including existing energy subsidies.
19 Real income is measured as the change in the consumer expenditure function (evaluated in base year prices), plus the change in real government expenditures. The changes are reported compared to the baseline scenario, and no discounting is involved.
20It is also worth noting that the Energy-exporting region (EEX) also benefits from the implementation of a more cost-efficient agreement.
21 See, for example, Burniaux et. al. (1993).
[SEDAC] [TOP]




